Para esta tarea se eligió el problema B.3.27 de la página
151 del libro [1]
El tema es diagrama de flujo de señales y las instrucciones
del ejercicio son:
-Obtenga la función de transferencia Y(s) / X(s) del sistema
que se muestra en la Figura 3.29
Y a continuación tenemos la figura:
Primero, podemos observar que hay 3 caminos directos entre
la entrada X(s) y la salida Y(s). Y las ganancias de estos caminos son:
Enseguida, determinamos los lazos que existen en el dibujo del problema:
Después, lo que hacemos es obtener el determinante Δ que esta dado por, si observamos los 3 Lazos tienen una rama en común, así que no hay lazos que no se tocan por lo tanto se suman, si existieran lazos que no se tocaran entonces estos se multiplicarían:
Sustituyendo nuestros valores en la ecuación obtenemos:
El cofactor Δ1
se obtiene a partir de Δ eliminando
los lazos que tocan el camino P1.
Por lo tanto, eliminamos L1,
L2 y L3 de la ecuación ya que estos lazos si tocan el
camino, y se obtiene:
Δ1 = 1
Y siguiendo con los demás también determinamos que ni para Δ2 ni tampoco para Δ3 con sus respectivos P2 y P3
son tocados, entonces también obtenemos:
Δ2 = 1 y Δ3 = 1
Para obtener nuestra función de transferencia o ganancia del sistema, tenemos la regla de la ganancia de Mason que esta determinada por:
La función de transferencia del problema es entonces:
El ultimo paso es solamente sustituir y obtenemos nuestra función de transferencia final.
Bibliografía:
[1] Automatización y control de sistemas dinámicos

.gif)
.gif)
.gif)
.gif)

.gif)

.gif)
.gif)
.gif)
.gif)

.gif)

.gif)


.gif)
.gif)



.gif)

.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

.gif)
.gif)
.gif)
.gif)
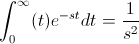
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

.png)





