Bueno esta es la función que me toco resolver:
Dada la condición de:
Primero
expresamos nuestra función aplicando la formula de Laplace. Esto sería la misma
solo con el símbolo que lo representa.
Separamos en dos la función e integramos con respecto a t ambos lados de la función usando las fórmulas que ya conocemos donde:
entonces,
y la segunda parte:
entonces,
La propiedad de estas formulas esta dada por:
Después al ya juntar las dos partes nos queda algo como esto:
igualmente aplicamos otra propiedad del lado izquierdo de la función para quitar la segunda derivada:
después de esto aplicamos el valor que nos da la descripción del problema, notar que "s" afecto a los demas términos también del lado derecho, lo que nos daría como resultado:
De nuevo aplicamos la propiedad que usamos al inicio, pero ahora de manera contraria para poder obtener la función casi terminada y podamos integrar directo, quedando como resultado:
Dejamos las constante fuera de la integral ya que esa no afecta, y después las expresamos como una sola:
Ya solamente eliminamos en ambos lados de la ecuación la integral y nos quedaría como resultado final lo siguiente:
Hacemos la comprobación
del problema en la aplicación de Wolfram Alpha. El resultado es el mismo, solo
cambiaron el orden de los valores con esto sabemos que el procedimiento
empleado es el correcto.
Y aquí esta la expresión gráfica de la función obtenida por Wolfram Alpha también:
Bibliografía:
http://faculty.atu.edu/mfinan/4243/Laplace.pdf
Apuntes de matemáticas IV
http://www.codecogs.com/latex/eqneditor.php
http://www.wolframalpha.com/

.gif)
.gif)
.gif)
.gif)
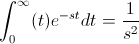
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

.png)
Los integrales sin especificación de variable están medio solitarios y creo que deberían ser L caligráficos. Te pongo 13 pts.
ResponderEliminar