Tarea 7 - Lógica Predicativa

En las actividades diarias humanas como los juegos en general, se suelen seguir reglas que son llamadas estrategias. Estos procesos en los juegos son sutiles, ya que son actividades que todos  conocemos y el objetivo es tener el mejor resultado posible dentro de un juego dependiendo de los distintos resultados que el juego tiene.

La relación entre la lógica y los juegos se remonta a la antigüedad donde surgió el contexto de la argumentación, donde los movimientos exitosos que los participantes podían hacer con seguridad. La argumentación es el juego donde siguiendo las reglas se puede perder o ganar dependiendo de la calidad de sus estrategias.

Y la estrategia que se a conocido desde hace mucho tiempo es que quien tiene lógicamente reclamaciones validas tiene una estrategia ganadora, garantizando el éxito a ganar.

Evaluación de los juegos en la lógica

Los movimientos de los juegos siguen la construcción inductiva de fórmulas, con dos jugadores V (verificador) y F (falsificador).

Disyunción ϕ1 v ϕ2

V elige el disyunción para jugar

Conjunción ϕ1 ^ ϕ2

F elige el conjunto para jugar

Negación ¬ϕ

Interrupción de roles entre los jugadores, el juego continua con respecto a

Cuantificador existencial   ∃x ϕ (x)

V toma un objeto d, y después el juego continua con respecto a

Cuantificador universal∀x ϕ (x)

El juego termina: Verificador gana si es verdad, falsificador gana si es falso.

Ejemplo:
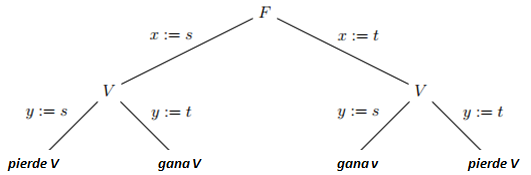
Se toman dos objetos: s, t. El juego de primer orden con sus movimientos representado en un árbol respecto a:   ∀x∃x ≠ y

Como podemos ver el primer movimiento lo hace F dando a V la opción de elegir de entre 4 opciones de las cuales dos para cada uno son para ganar.. Pero aquí es donde se muestra la ventaja para V porque solo de el depende que el gane, sin importar el movimiento que haya hecho F.

Ejemplo 2:
Con esto veamos este pequeño ejemplo clásico el juego del "gato" donde hay 2 jugadores y el objetivo es obtener 3 de las mismas figuras en la misma dirección el primero que lo logre gana.

De acuerdo al escenario planteado, vemos las posibilidades de cada uno de los dos jugadores gracias a un árbol y obtenemos quien tiene mas probabilidad de éxito.

Como se puede observar de acuerdo a la opción inicial fueron desenvolviéndose las opciones de cada escenario posible para así concluir quien tiene mas probabilidades de éxito y como ganar al juego, si cada jugador conociera y estas posibilidades podría ir siguiendo las reglas de la lógica proposicional y así conocer que movimiento hacer. Este ejemplo se resuelve por el algoritmo de Zermelo , al igual que otros juegos como el del ajedrez.

Bibliografía:   http://www.logicinaction.org/docs/ch7.pdf