Asignación de polos.
Un método de diseño conocido comúnmente como técnica de ubicación o de asignación de polos. Se supone que todas las variables de estado son medibles y que están disponibles para su realimentación.
Diseño mediante asignación de polos.
En el enfoque convencional del diseño de un sistema de control con una sola entrada y una sola salida, se diseña un controlador (compensador) tal que los polos dominantes en lazo cerrado tengan una razón de amortiguamiento y una frecuencia natural no amortiguada w deseada. En este método, el orden del sistema aumenta en 1 o 2, a menos que ocurra una cancelación de polos.
Observadores de estado. Condición necesaria y suficiente para la observación del estado
Una condición necesaria y suficiente para la determinación de la matriz de ganancias del observador K para los valores propios deseados de A-K*C es que el dual del sistema original sea de estado completamente controlable. La condición de controlabilidad completa del estado para este sistema dual es que el rango de sea n.
Ésta es la condición para una observabilidad completa del sistema original definido. Esto significa que una condición necesaria y suficiente para la observación del estado del sistema definido que es el sistema sea completamente observable.
Una ves que se han seleccionado los valores propios deseados (o la ecuación característica deseada), se puede diseñar el observador de estado de orden completo, si la planta es completamente observable. Los valores propios deseados de la ecuación características se deberían escoger de forma que el observador de estado responda al menos de dos a cinco veces más rápido que el sistema en lazo cerrado considerado.
Problema
B.12.11
Página. 949
Sea el proceso definido por:
.gif)
.gif)
donde:
Diseñe un orden de estado en orden completo, suponiendo que los polos deseados por el observador son:
Respuesta
El problema de asignación de polos se solucionan fácilmente con el comando acker o place . Yo en este caso utilizó el de place para el calculo de la matriz de ganancias de realimentación k.
Para esto:
x = vector de estado (n-vector)
y = señal de salida
u = señal de control
A = n x n constante de matriz
B = n x 1 constante de matriz
C = 1 x n constante de matriz
Polos:
Determinando la matriz de ganancia de realimentación del estado K con octave.
Aquí esta el programa que utilizo para generar la matriz K. Yo utilice la función place porque en octave no se puede la función acker.
Obtenemos: 35.0000, 394.0000, 1285.0000
.gif) |
| Ec. para el observador de estado de orden completo |
Los valores propios deseados de la ecuación característica se deberían escoger de forma que el observador de estado responda al menos de dos a cinco veces más rápido que el sistema en lazo cerrado considerado.
Se observa que hasta ahora se ha puesto que las matrices A, B y C en el observador son exactamente iguales a las de la planta física.
De acuerdo a la ecuación para el observador de estado de orden completo determinamos:
Sustituyendo todas las variables obtenemos el resultado final:
.gif) |
| Ec. para el observador sustituido |
Código
Bibliografía
Libro Ingeniería de Control Moderna
http://octave.sourceforge.net/control/function/place.html
http://rosettacode.org/wiki/Ackermann_function#Octave
.gif)
.gif)
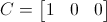.gif)
.gif)

.gif)
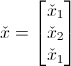.gif)
OK; 15.
ResponderEliminar